TNotes.canvas

Appearance

to top

0025. 使用 ctx.quadraticCurveTo、ctx.bezierCurveTo 绘制贝塞尔曲线 ​

  • ctx.quadraticCurveTo、ctx.bezierCurveTo 这俩 API 的使用很简单，无非就是传入 2 个点还是 3 个点。重点在于理解贝塞尔曲线的绘制原理。理解原理后，自然就理解这俩 API 应该如何使用了。
  • https://blog.csdn.net/m0_37602827/article/details/118165217 - CSDN - 贝塞尔曲线原理 - 这是 CSDN 上的一篇介绍贝塞尔曲线原理的文章。

1. 📒 二次、三次贝塞尔曲线绘制原理 ​

  • 贝塞尔曲线的相关内容，是个通用的知识点，在学习 canvas、svg、css 等跟 UI 绘图相关的技术时都会接触到。
    • 在 canvas、svg 中，我们通过指定起点、终点和控制点的坐标，来绘制二次、三次贝塞尔曲线。
    • 在 css 中，我们也可以通过 chrome devtools 来手动调节动画效果或过渡效果的变化贝塞尔曲线。
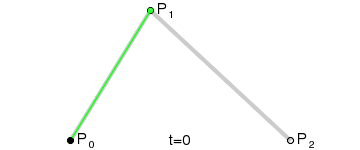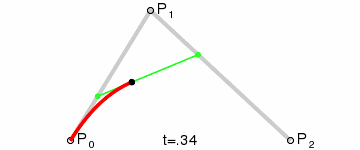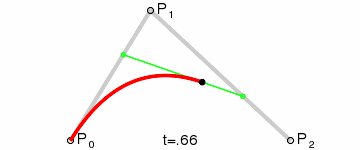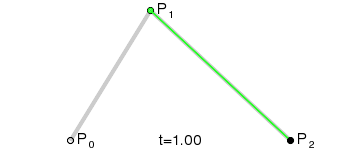
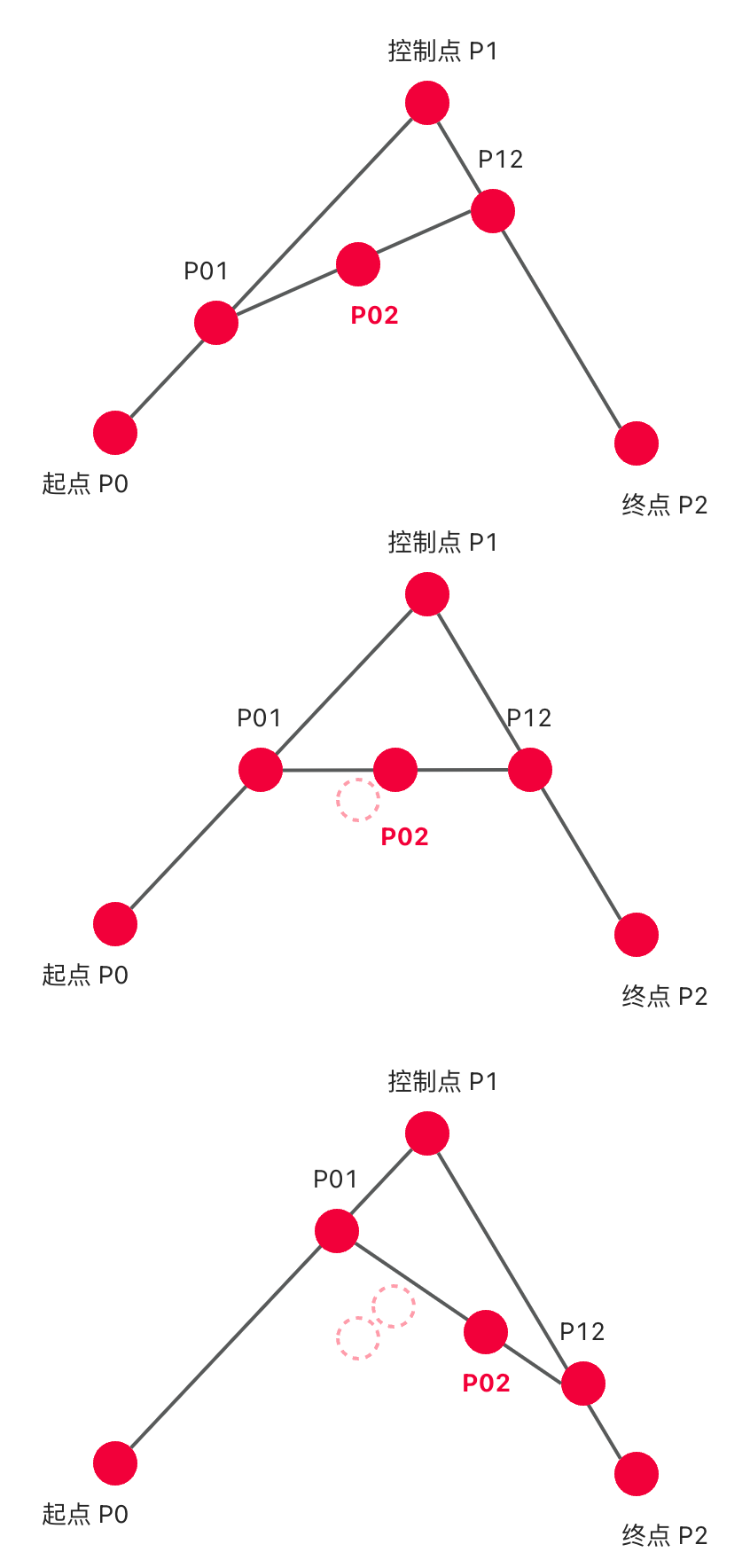
  • 二次贝塞尔曲线的绘制原理
    • 假设：
      • x1 = P0，P01 之间的距离
      • x2 = P0，P1 之间的距离
      • x3 = P1，P12 之间的距离
      • x4 = P1，P2 之间的距离
      • x5 = P01，P02 之间的距离
      • x6 = P01，P12 之间的距离
    • 存在一个参数 t，使得上述 x 满足以下条件：
      • t = x1 / x2
      • t = x3 / x4
      • t = x5 / x6
    • 按照上述规则不难想象，如果 t 是 0，那么 P02 位于起点 P0 位置；如果 t 是 1，那么 P02 位于终点 P2 位置。当 t 介于 0-1 之间时，可以通过上述规则找到 P02 点的位置。这意味着，当 t 从 0 变到 1 时，会获得无数个 P02 点，这就形成了一个光滑的曲线 —— 由无数个 P02 点连成的曲线。
    • 上述就是二次贝塞尔曲线的绘制原理。
  • 三次贝塞尔曲线绘制原理
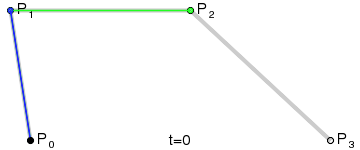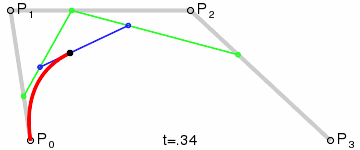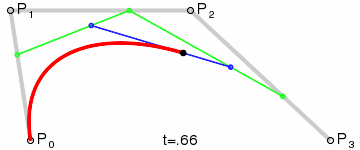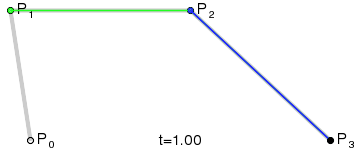
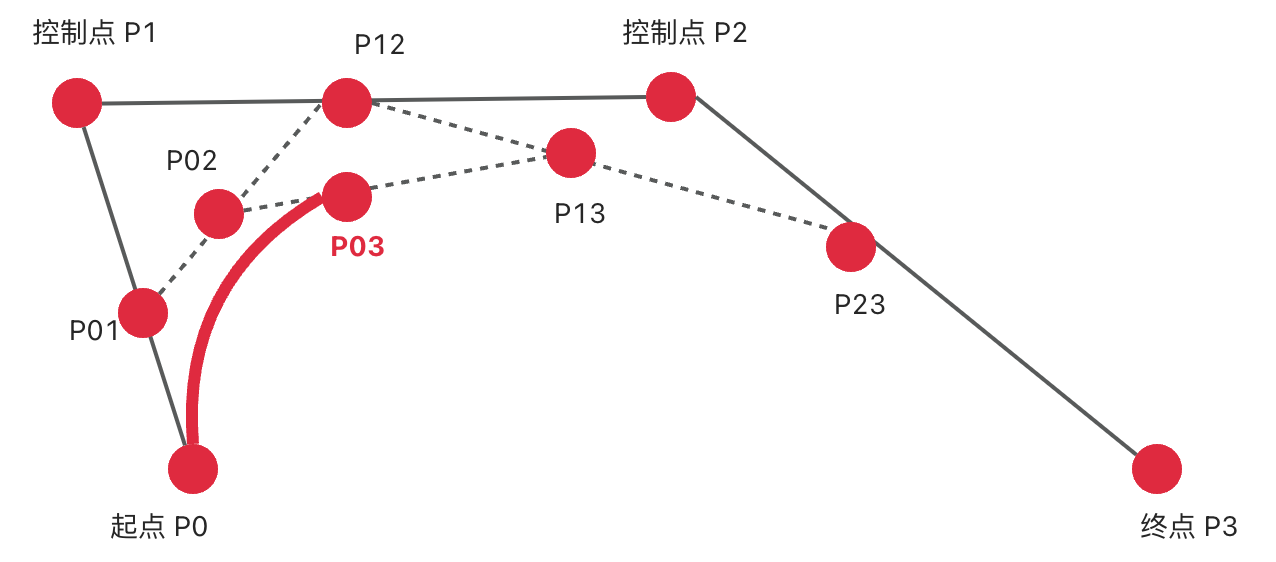
    • 二次贝塞尔曲线有一个控制点，三次贝塞尔曲线有两个控制点。在理解了二次贝塞尔曲线的绘制原理后，找葫芦画瓢，三次也是一样的。
    • 假设：
      • x1 = P0，P01 之间的距离
      • x2 = P0，P1 之间的距离
      • x3 = P1，P12 之间的距离
      • x4 = P1，P2 之间的距离
      • x5 = P01，P02 之间的距离
      • x6 = P01，P12 之间的距离
      • x7 = P2，P23 之间的距离
      • x8 = P2，P3 之间的距离
      • x9 = P12，P13 之间的距离
      • x10 = P12，P23 之间的距离
    • 存在一个参数 t，使得上述 x 满足以下条件：
      • t = x1 / x2
      • t = x3 / x4
      • t = x5 / x6
      • t = x7 / x8
      • t = x9 / x10
    • 按照上述规则不难想象，如果 t 是 0，那么 P03 位于起点 P0 位置；如果 t 是 1，那么 P03 位于终点 P3 位置。当 t 介于 0-1 之间时，可以通过上述规则找到 P03 点的位置。这意味着，当 t 从 0 变到 1 时，会获得无数个 P03 点，这就形成了一个光滑的曲线 —— 由无数个 P03 点连成的曲线。

上述就是三次贝塞尔曲线的绘制原理。

2. 💻 demos.1 - 二次贝塞尔曲线 ​

html
<!-- 1.html -->
<!DOCTYPE html>
<html lang="en">
  <head>
    <meta charset="UTF-8" />
    <meta name="viewport" content="width=device-width, initial-scale=1.0" />
    <title>Document</title>
  </head>
  <body>
    <script src="./drawGrid.js"></script>
    <script>
      const cavnas = document.createElement('canvas')
      drawGrid(cavnas, 500, 500, 50)
      document.body.appendChild(cavnas)
      const ctx = cavnas.getContext('2d')

      ctx.fillStyle = 'red'

      ctx.beginPath()
      ctx.arc(50, 200, 4, 0, Math.PI * 2) // 起点
      ctx.fill()
      ctx.beginPath()
      ctx.arc(100, 100, 4, 0, Math.PI * 2) // 控制点
      ctx.fill()
      ctx.beginPath()
      ctx.arc(250, 200, 4, 0, Math.PI * 2) // 终点
      ctx.fill()

      // ctx.quadraticCurveTo(cpx, cpy, x, y)
      // 使用 ctx.quadraticCurveTo 方法绘制二次贝塞尔曲线

      // cpx cpy 表示控制点坐标
      // x y 表示终点坐标

      // 起点坐标是 moveTo 设置，或者是上一次绘图的结尾。

      ctx.beginPath()
      ctx.moveTo(50, 200)
      ctx.quadraticCurveTo(100, 100, 250, 200)
      ctx.stroke()
    </script>
  </body>
</html>

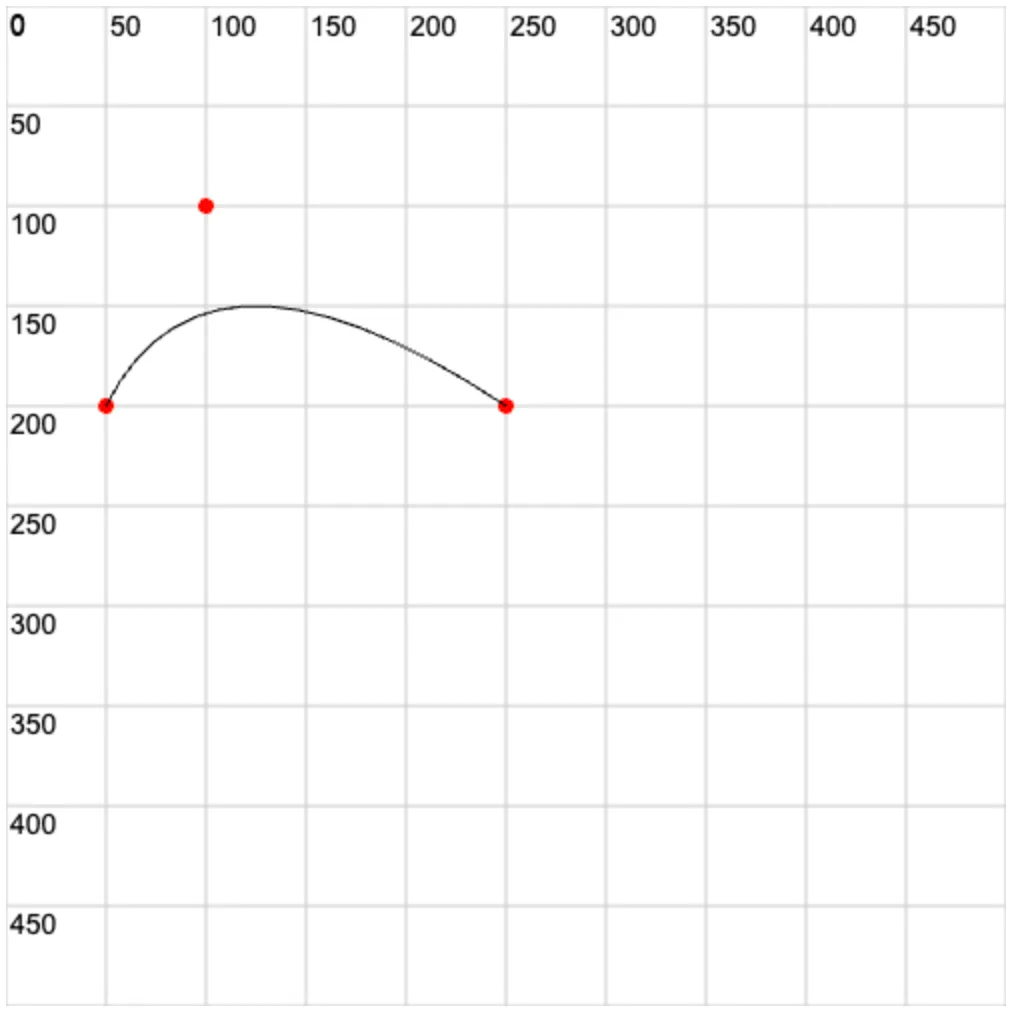
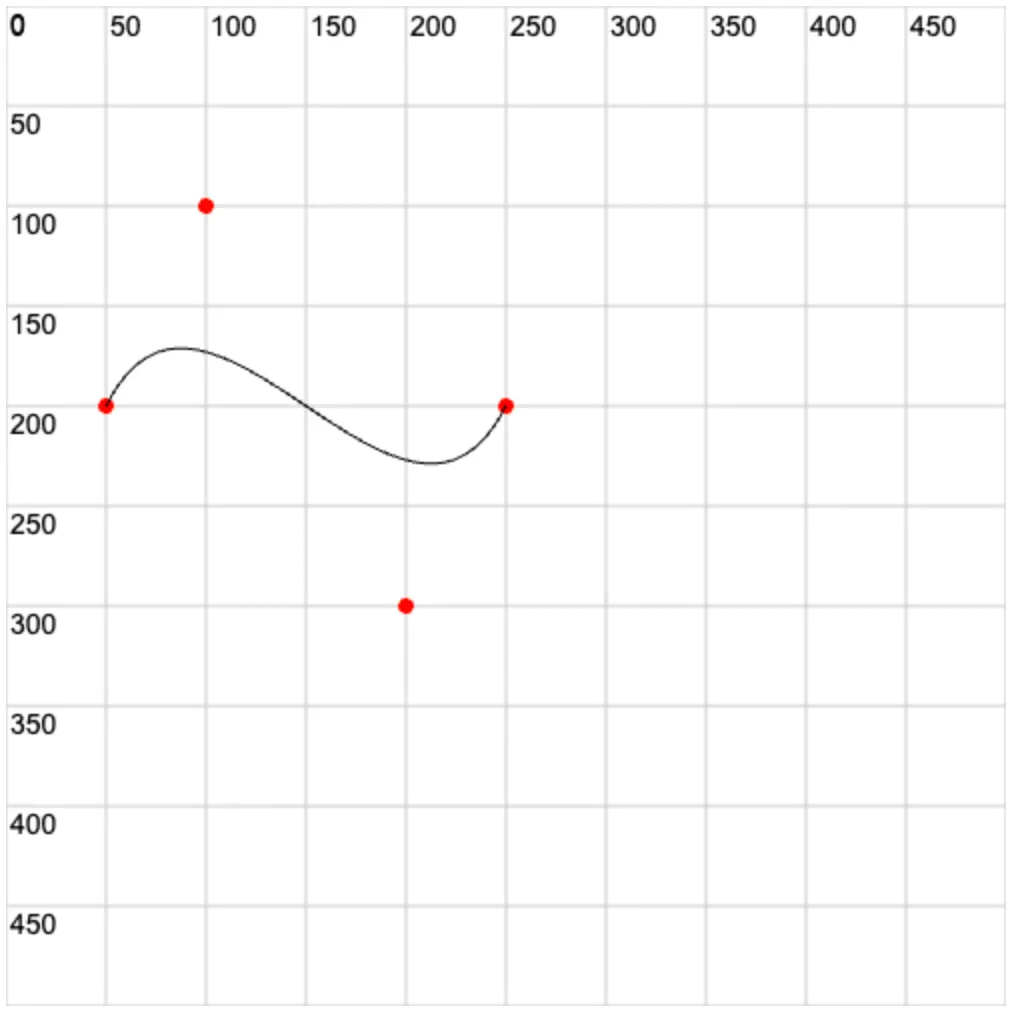
3. 💻 demos.2 - 三次贝塞尔曲线 ​

html
<!-- 2.html -->
<!DOCTYPE html>
<html lang="en">
  <head>
    <meta charset="UTF-8" />
    <meta name="viewport" content="width=device-width, initial-scale=1.0" />
    <title>Document</title>
  </head>
  <body>
    <script src="./drawGrid.js"></script>
    <script>
      const cavnas = document.createElement('canvas')
      document.body.appendChild(cavnas)
      drawGrid(cavnas, 500, 500, 50)
      const ctx = cavnas.getContext('2d')
      ctx.beginPath()

      ctx.fillStyle = 'red'

      ctx.arc(50, 200, 4, 0, Math.PI * 2) // 起点
      ctx.fill()
      ctx.beginPath()
      ctx.arc(100, 100, 4, 0, Math.PI * 2) // 控制点 1
      ctx.fill()
      ctx.beginPath()
      ctx.arc(200, 300, 4, 0, Math.PI * 2) // 控制点 2
      ctx.fill()
      ctx.beginPath()
      ctx.arc(250, 200, 4, 0, Math.PI * 2) // 终点
      ctx.fill()

      // ctx.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y)
      // 使用 ctx.bezierCurveTo 方法绘制三次贝塞尔曲线

      // 起点坐标是 moveTo 设置，或者是上一次绘图的结尾。
      // cp1x cp1y 表示控制点 1 坐标
      // cp2x cp2y 表示控制点 2 坐标
      // x y 表示终点坐标

      ctx.beginPath()
      ctx.moveTo(50, 200)
      ctx.bezierCurveTo(100, 100, 200, 300, 250, 200)
      ctx.stroke()
    </script>
  </body>
</html>