TNotes.leetcode

Appearance

to top

0153. 寻找旋转排序数组中的最小值【中等】 ​

1. 🔗 links ​

2. 📝 Description ​

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 3 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

  • n == nums.length
  • 1 <= n <= 5000
  • -5000 <= nums[i] <= 5000
  • nums 中的所有整数 互不相同
  • nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

3. 💻 题解.1 - 双指针1 ​

js
/**
 * 22-10-12
 * @param {number[]} nums
 * @return {number}
 */
var findMin = function(nums) {
  const len = nums.length

  if (len === 1) return nums[0]

  let slow = 0, fast = 1

  while (fast < len) {
    if (nums[slow] > nums[fast]) return nums[fast]
    // 继续走
    fast++
    slow++
  }

  return nums[0]
};
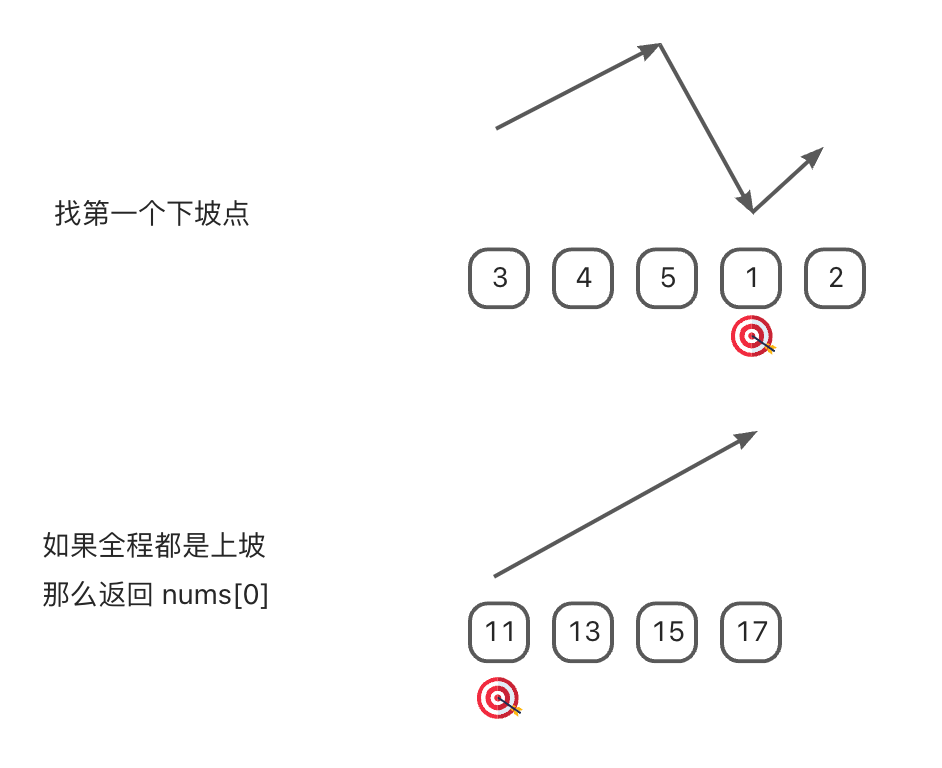
  • 图解：

4. 💻 题解.2 - 二分查找 ​

js
/**
 * 22-10-12
 * @param {number[]} nums
 * @return {number}
 */
var findMin = function(nums) {
  const n = nums.length
  if (n === 1) return nums[0]

  let low = 0, high = n - 1, pivot = low + ((high - low) >> 1)
  while (low < high) {
    if (nums[pivot] < nums[high]) high = pivot
    else low = pivot + 1
    pivot = low + ((high - low) >> 1)
  }
  
  return nums[pivot]
};
  • 图解：
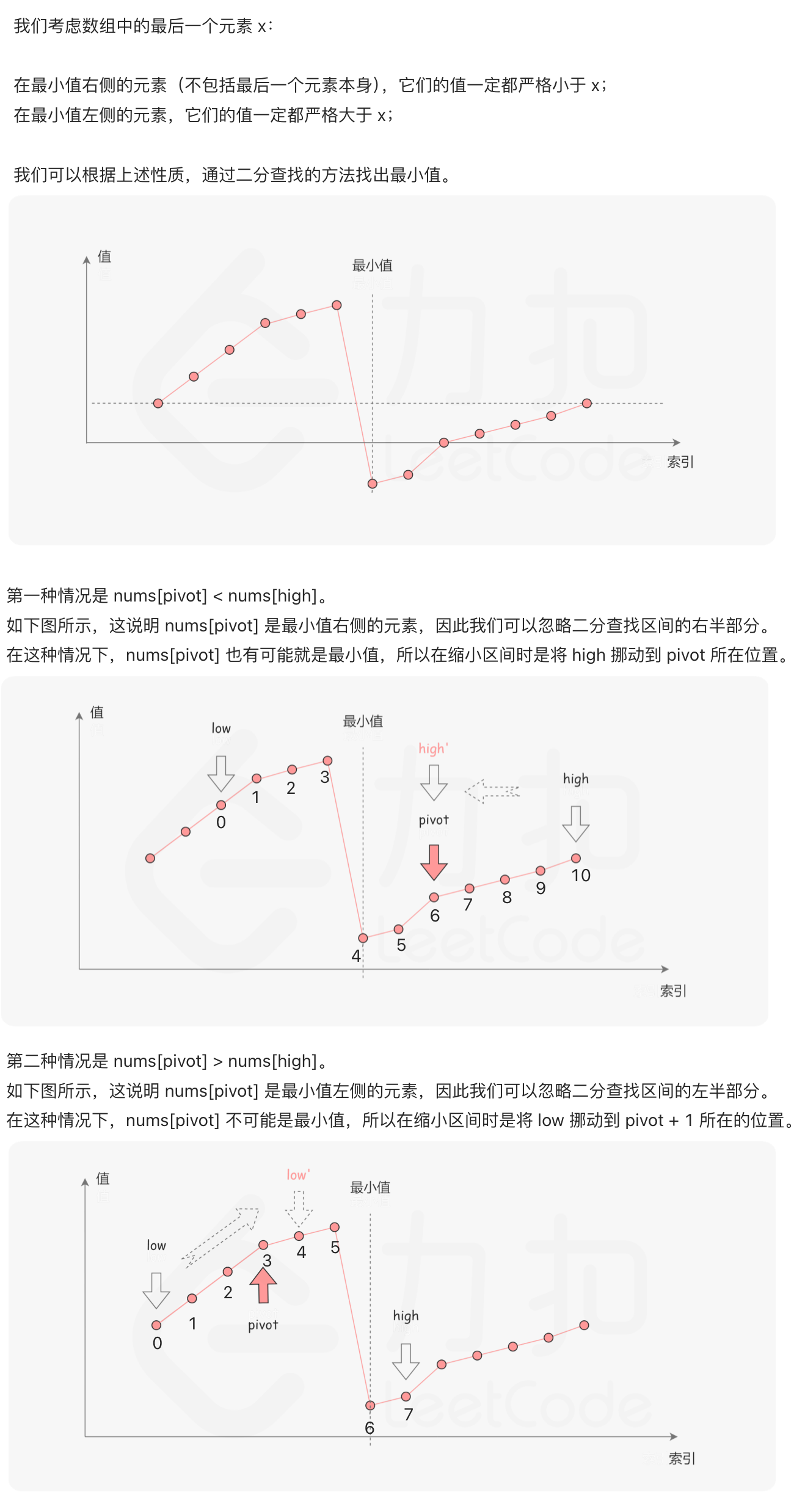
    • 注意：题目描述中提到每一个元素都是不相同的，因此在比较的时候，不可能存在相等的情况。
  • 🤔 思考： 为什么当两个指针相撞退出循环的时候，pivot 指向的一定就是最小值呢？
    • 当执行到 return nums[pivot] 语句的时候，low、high、pivot 都是相等的，此时区间已经缩小到了只有一个成员，所以返回 nums[pivot] 就是最小值，返回 nums[low]、nums[high] 也都是可以的。
  • 🤔 思考： 为什么当两个指针相撞的时候，一定是 low === high 呢？有没有可能会是 low 指向了 high 右边的值，low === high + 1 呢？
    • 特殊情况：n = 1，这时候不需要讨论，直接返回 nums[0] 即可。
    • 普遍情况：区间的每次缩小，都是对半砍的，倒数第二步一定会收缩到只有两个成员的情况。
      • 这时候无非左边的大于右边，或者右边的大于左边，无论是哪种情况，最后一次遍历结束后，low、high、pivot 三者一定会变为相等的。你可以假设 nums = [0, 1] 或者 nums = [0, 1] 代入到程序中想想执行流程。
  • 补充：
    • 首次计算 pivot 的时候 pivot = low + ((high - low) >> 1) 可以简写为 pivot = high >> 1
    • 本题中的 pivot = low + ((high - low) >> 1) 可以简写为 pivot = (high + low) >> 1
js
var findMin = function(nums) {
  const n = nums.length
  if (n === 1) return nums[0]

  let low = 0, high = n - 1, pivot = high >> 1
  while (low < high) {
    if (nums[pivot] < nums[high]) high = pivot
    else low = pivot + 1
    pivot = (high + low) >> 1
  }

  return nums[pivot]
}

5. 🤖 AI - pivot = low + ((high - low) >> 1)、pivot = (high + low) >> 1 这两种写法等效吗？ ​

这两种写法在大多数情况下是等效的，但它们在某些边界情况下可能会有不同的表现。让我们详细分析一下这两种写法的差异和等效性。

5.1. pivot = low + ((high - low) >> 1) ​

这种写法是为了防止整数溢出。在某些编程语言中，特别是当 low 和 high 都是大整数时，high + low 可能会导致整数溢出。为了避免这种情况，使用 low + ((high - low) >> 1) 可以确保计算结果不会溢出。

5.1.1. 优点 ​

  • 防止整数溢出：适用于大整数的情况，避免 high + low 导致的溢出。

5.1.2. 缺点 ​

  • 稍微复杂：相对于 (high + low) >> 1，这种写法稍微复杂一些。

5.2. pivot = (high + low) >> 1 ​

这种写法更简洁，直接计算 low 和 high 的平均值并右移一位（相当于除以 2）。

5.2.1. 优点 ​

  • 简洁：代码更简洁，易于理解。

5.2.2. 缺点 ​

  • 可能溢出：在某些编程语言中，当 low 和 high 都是大整数时，high + low 可能会导致整数溢出。

5.3. 等效性分析 ​

在大多数情况下，这两种写法是等效的，因为它们都计算的是 low 和 high 的中间位置。具体来说：

  • 对于非负整数：在大多数实际应用中，low 和 high 都是非负整数，且不会导致溢出。在这种情况下，这两种写法是完全等效的。
  • 对于负整数：在某些情况下，如果 low 和 high 是负整数，两种写法可能会有不同的结果，但这种情况在实际应用中很少见。

5.4. 示例 ​

假设 low = 2 和 high = 8：

  1. pivot = low + ((high - low) >> 1)：

    • high - low = 8 - 2 = 6
    • (high - low) >> 1 = 6 >> 1 = 3
    • pivot = low + 3 = 2 + 3 = 5

  2. pivot = (high + low) >> 1：

    • high + low = 8 + 2 = 10
    • (high + low) >> 1 = 10 >> 1 = 5

在这两种情况下，pivot 都是 5，结果是相同的。

5.5. 结论 ​

  • 大多数情况下等效：在大多数实际应用中，这两种写法是等效的。
  • 防止溢出：如果你担心整数溢出，特别是当 low 和 high 都是大整数时，建议使用 pivot = low + ((high - low) >> 1)。
  • 简洁性：如果你确定不会发生溢出，可以使用 pivot = (high + low) >> 1，因为它更简洁。