0003. 无重复字符的最长子串【中等】

📂 TNotes.yuque
- TNotes.yuque.leetcode.0003
1. 📝 Description
2. 💻 solutions.1 - 暴力解法
3. 💻 solutions.2 - 滑动窗口

1. 📝 Description

leetcode

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

子字符串 是字符串中连续的非空字符序列。

示例 1:

输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。请注意，你的答案必须是子串的长度，"pwke" 是一个子序列，不是子串。

提示：

0 <= s.length <= 5 * 10^4
s 由英文字母、数字、符号和空格组成

2. 💻 solutions.1 - 暴力解法

1.js1.ts

var lengthOfLongestSubstring = function (s) {
  const len = s.length,
    set = new Set()
  let ans = 0
  for (let i = 0; i < len; i++) {
    // start
    for (let j = i; j < len; j++) {
      // end
      if (!set.has(s[j])) {
        set.add(s[j])
        ans = ans > set.size ? ans : set.size
      } else {
        set.clear()
        break // start 右移
      }
    }
  }
  return ans
}

function lengthOfLongestSubstring(s: string): number {
  const len = s.length
  const set = new Set<string>()
  let ans = 0

  for (let i = 0; i < len; i++) {
    // start
    for (let j = i; j < len; j++) {
      // end
      if (!set.has(s[j])) {
        set.add(s[j])
        ans = ans > set.size ? ans : set.size
      } else {
        set.clear()
        break // start 右移
      }
    }
  }

  return ans
}

Details

时间复杂度： $O (n^{2})$
空间复杂度： $O (n)$
原理简述
- start 表示每次扫描的开始位置，end 表示每次扫描的结束位置，end 每次出生的位置就是 start 所在的位置。在每次扫描的过程中，start 不动，end 不断向右偏移，end 已经扫过的区域都加入到 set 中记录起来。
- 如果 end 位置的字符在 set 中出现过，那么将 set 清空，开启下一次扫描。此时退出内层循环，start 向右偏移。
- 如果 end 位置的字符在 set 中没有出现过，那么将该字符加入 set 中，并记录最长子串的长度。
流程分析
1. 初始化变量：
  - len：保存字符串 s 的长度。
  - set：一个用于存储字符的 Set 集合，用于检查子串中是否有重复字符。
  - ans：用于记录最长无重复字符子串的长度，初始值为 0，也是该函数最终返回的结果。
    - 为什么要初始为 0？
    - 特殊情况：s = "" 输入的 s 为空字符串，此时将不会进入循环，因此需要注意将 ans 的初始值设置为 0。
2. 双层循环遍历字符串：
  - 外层循环 for (let i = 0; i < len; i++)：i 表示子串的起始位置。
  - 内层循环 for (let j = i; j < len; j++)：j 表示子串的结束位置，每次 j 扫描过的区域就是从当前 i 位置开始的最长子串。
3. 检查子串中的字符：
  - 在内层循环中，检查当前字符 s[j] 是否已经存在于 set 中。
  - 如果当前字符不在 set 中：
    - 将字符 s[j] 添加到 set 中。
    - 更新 ans 的值为 set.size 和 ans 中的较大者。
  - 如果当前字符已经在 set 中：
    - 清空 set，表示需要重新开始寻找新的子串。
    - 使用 break 跳出内层循环，继续外层循环，以 i+1 为新的起始位置重新寻找子串。
4. 返回结果：
  - 外层循环结束后，返回 ans，即最长无重复字符子串的长度。
示例执行流程
- 假设输入字符串为 "abcabcbb"。
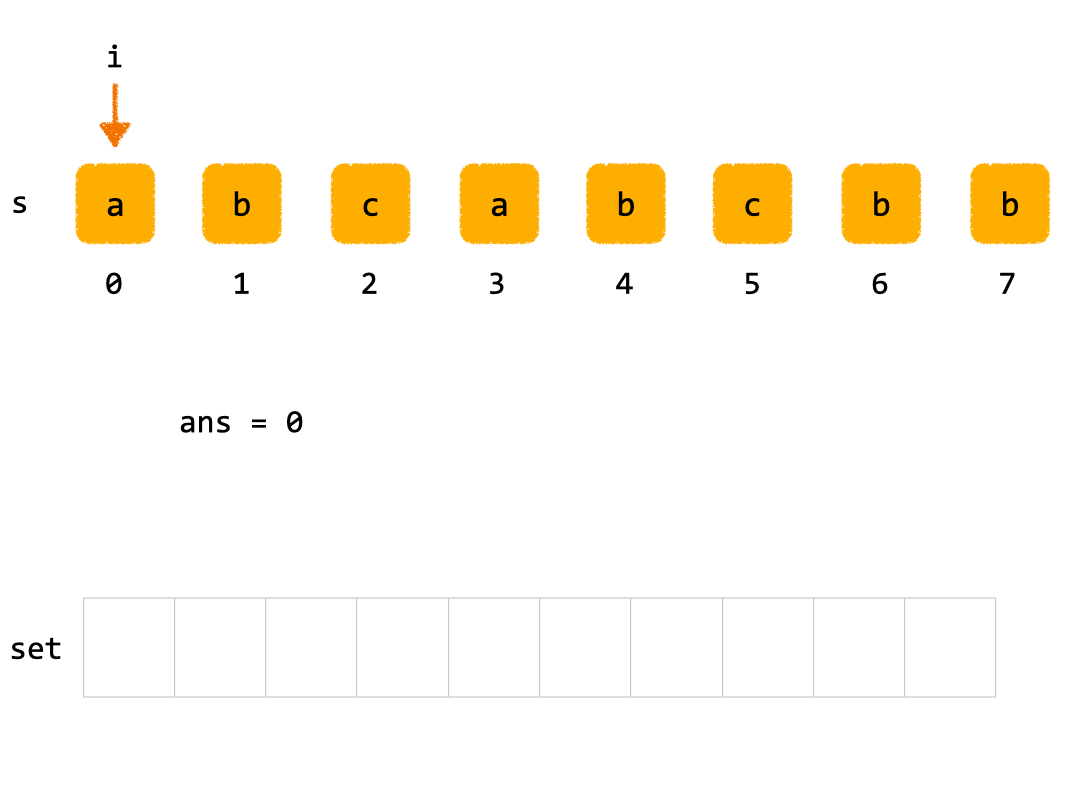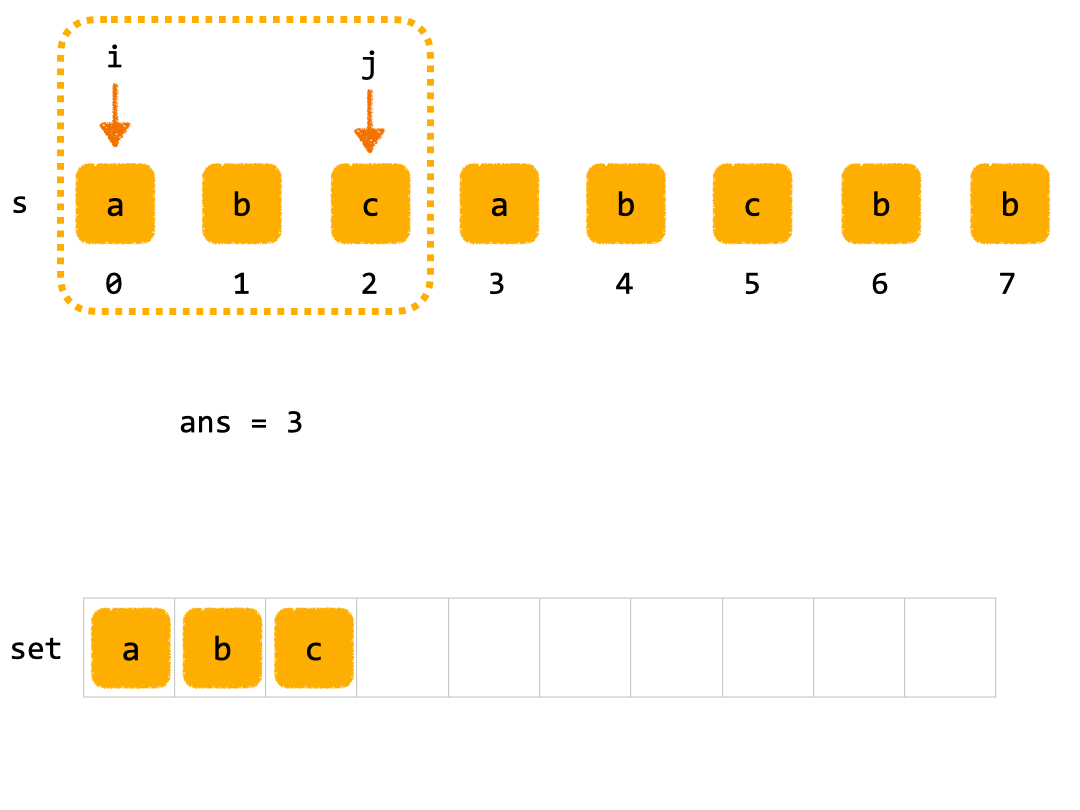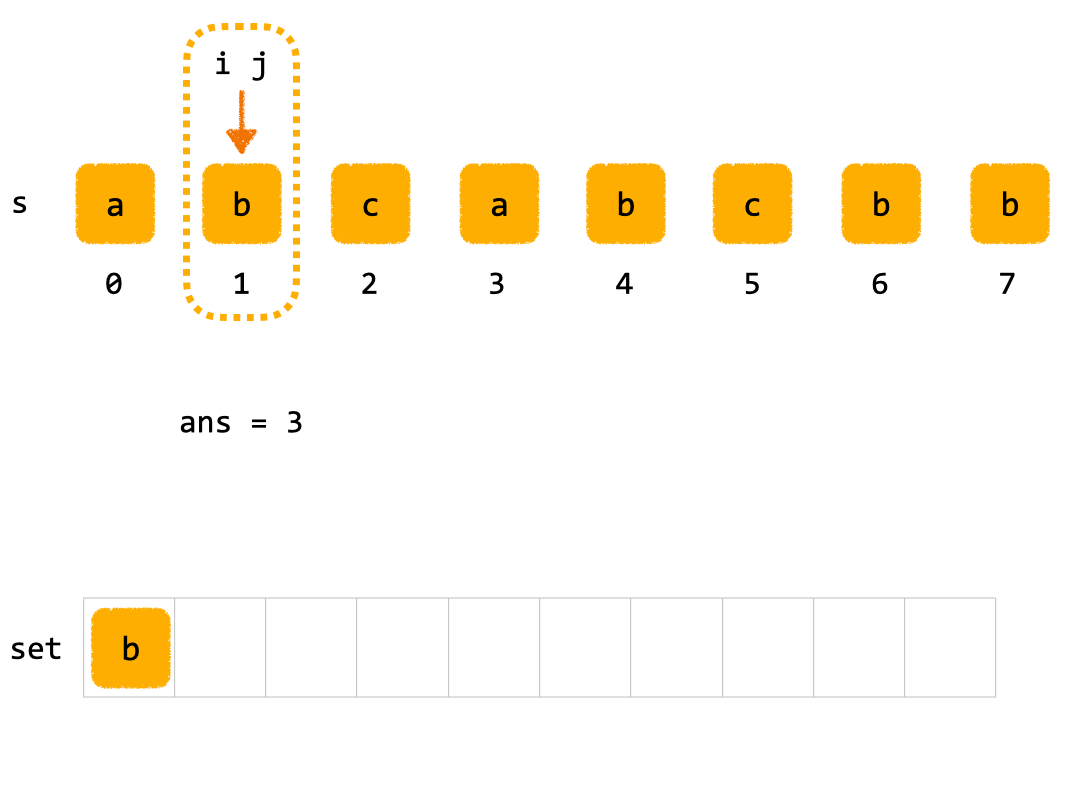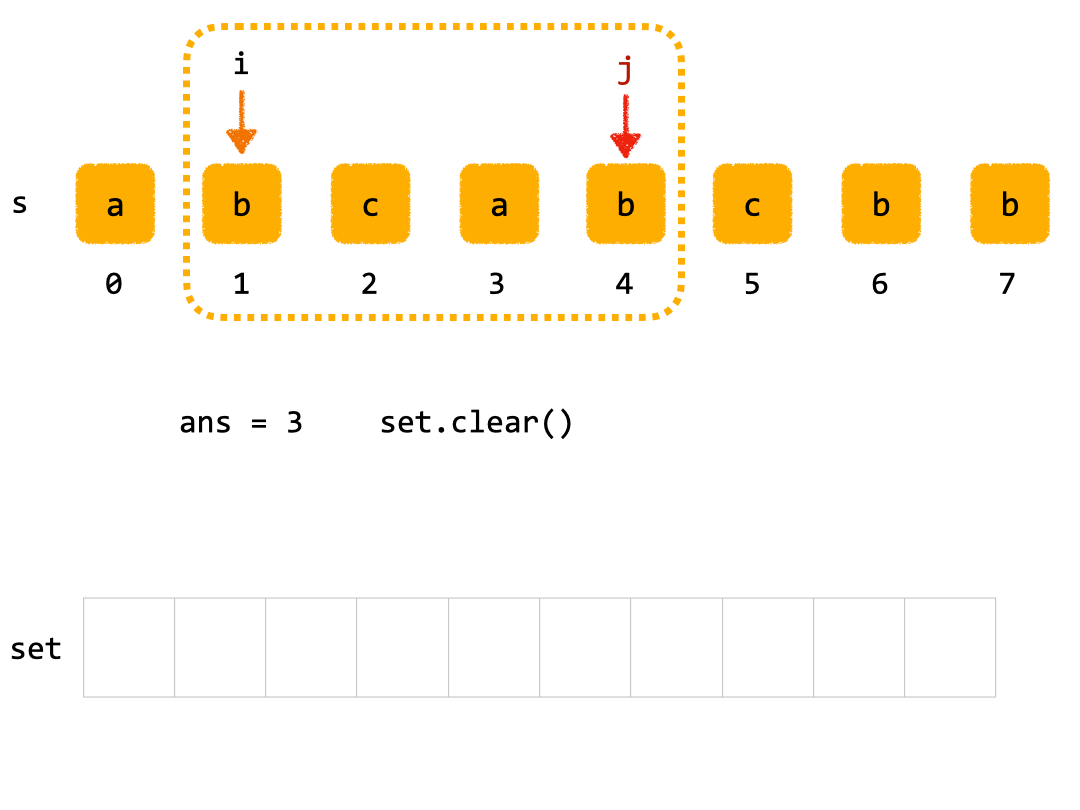
1. 初始状态：
  - len = 8
  - set = new Set()
  - ans = 0
2. 外层循环（起始位置 i 从 0 开始）：
  - 第一轮内层循环（起始位置 i = 0）：
    - j = 0，字符 a 不在 set 中，添加到 set，set = {'a'}，更新 ans = 1。
    - j = 1，字符 b 不在 set 中，添加到 set，set = {'a', 'b'}，更新 ans = 2。
    - j = 2，字符 c 不在 set 中，添加到 set，set = {'a', 'b', 'c'}，更新 ans = 3。
    - j = 3，字符 a 在 set 中，清空 set，跳出内层循环。
  - 第二轮内层循环（起始位置 i = 1）：
    - j = 1，字符 b 不在 set 中，添加到 set，set = {'b'}，更新 ans = 3。
    - j = 2，字符 c 不在 set 中，添加到 set，set = {'b', 'c'}，更新 ans = 3。
    - j = 3，字符 a 不在 set 中，添加到 set，set = {'b', 'c', 'a'}，更新 ans = 3。
    - j = 4，字符 b 在 set 中，清空 set，跳出内层循环。
  - 第三轮内层循环（起始位置 i = 2）：
    - 以此类推... 直到外层循环结束，将找到无重复的最长子串返回。
如何改进
- set.clear() 每次遇到重复字符后，集合会被清空，可能丢失之前已经统计的有效子串。
- **思考切入点：**如何让收集到的子串能够被充分利用起来，不要每次都清空，然后从 0 继续开始收集。
  - 通过使用滑动窗口和哈希集合，可以优化为线性时间复杂度 O(n)。

3. 💻 solutions.2 - 滑动窗口

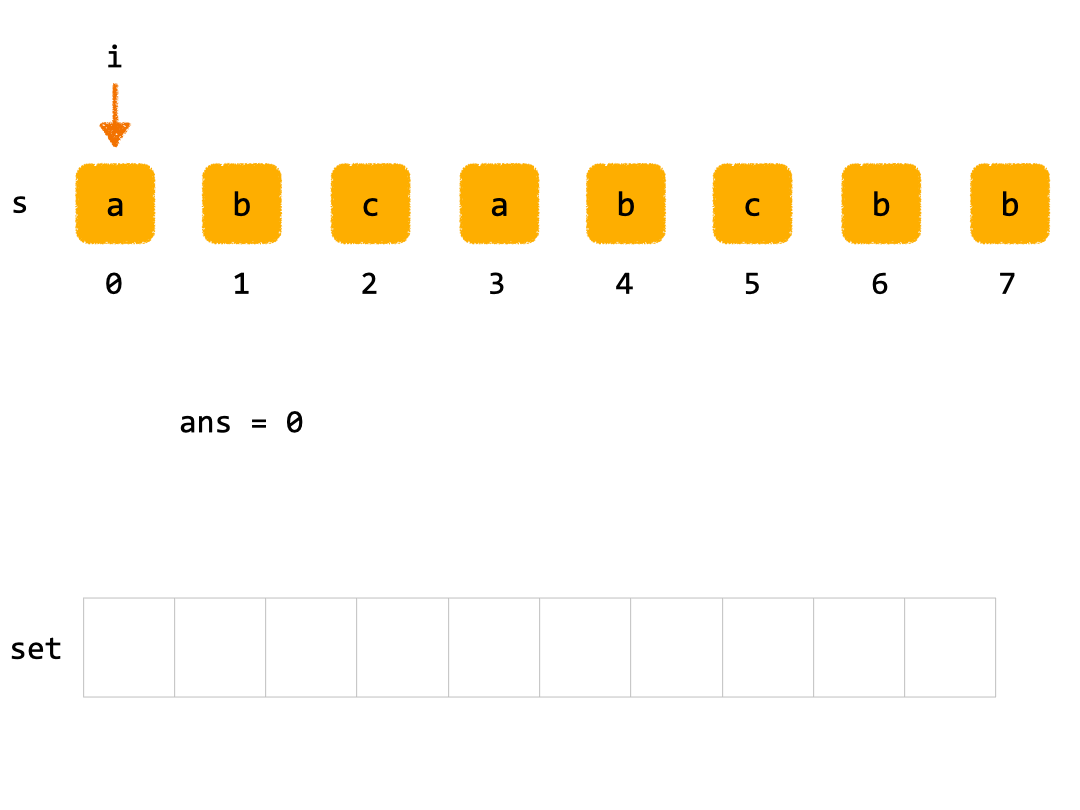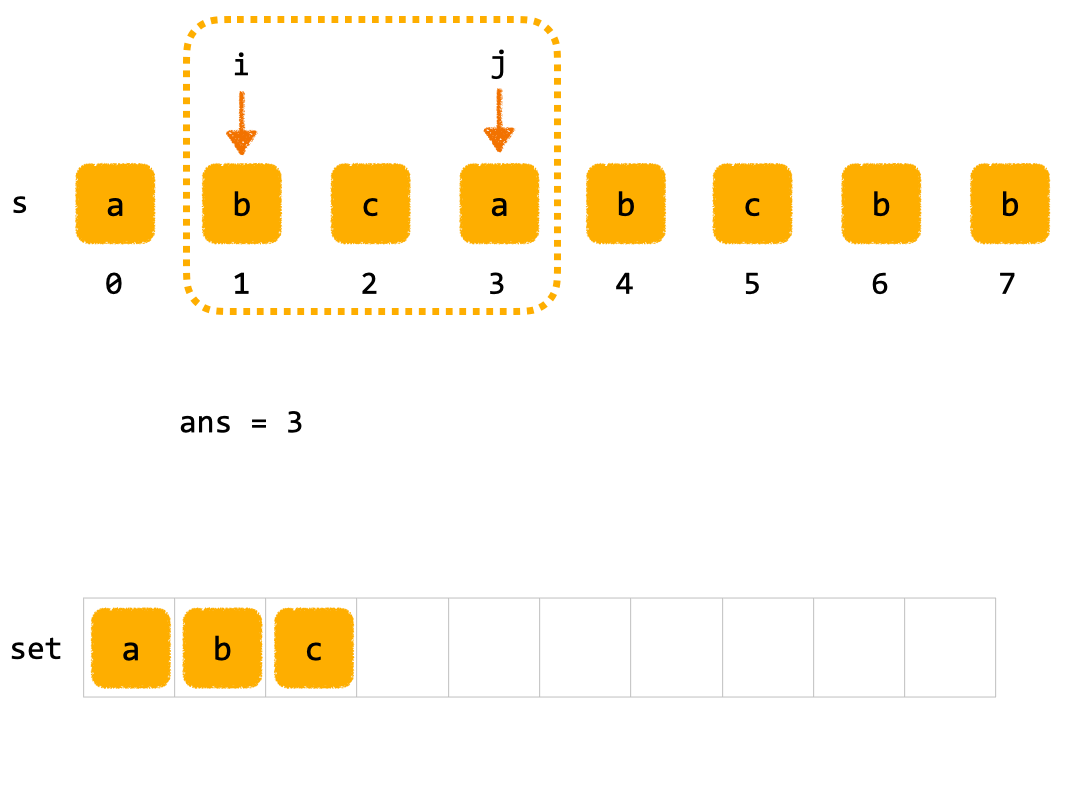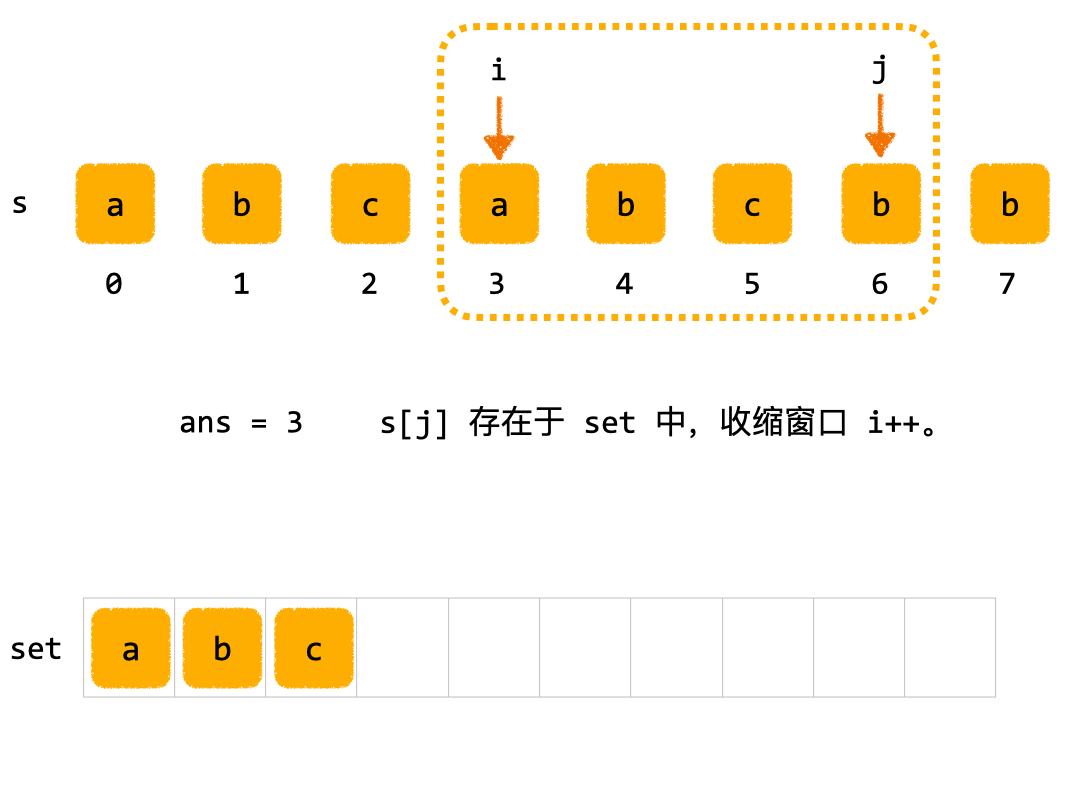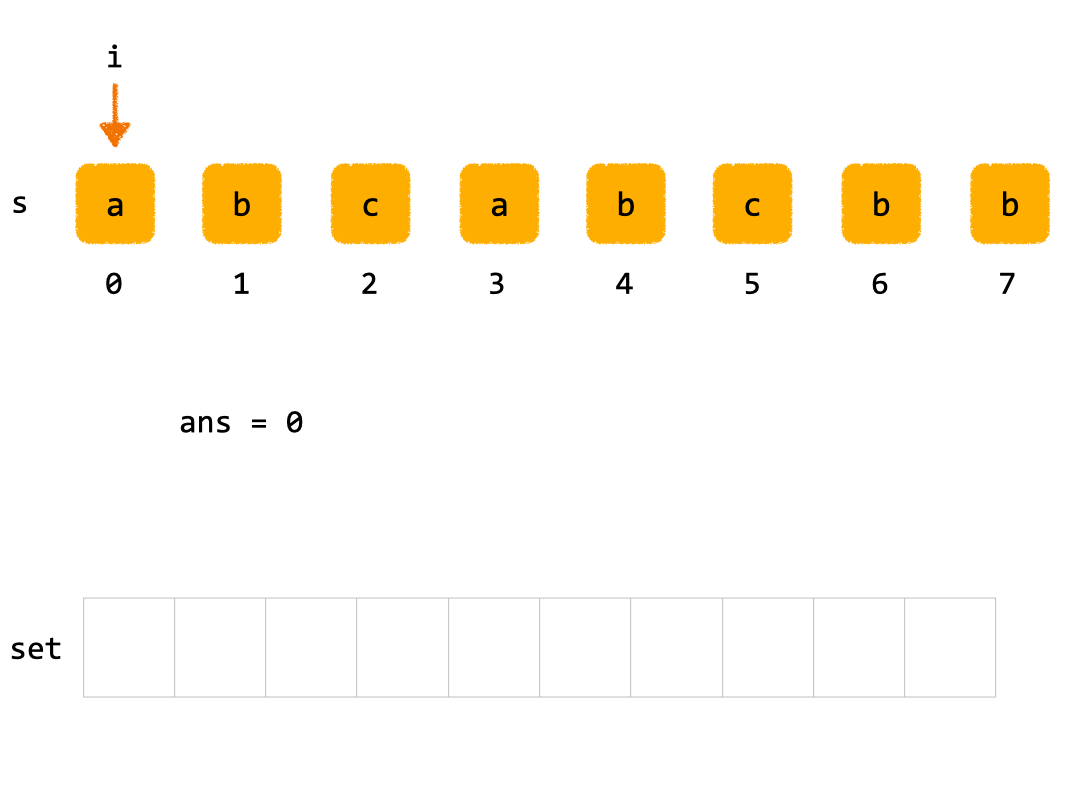
1.js2.js1.ts

var lengthOfLongestSubstring = function (s) {
  const len = s.length
  const set = new Set()

  let ans = 0
  let left = 0
  let right = 0

  while (right < len) {
    if (!set.has(s[right])) {
      set.add(s[right])
      right++
      ans = Math.max(ans, set.size)
    } else {
      set.delete(s[left])
      left++
    }
  }
  return ans
}

var lengthOfLongestSubstring = function (s) {
  const len = s.length
  const set = new Set()

  let ans = 0
  let end = -1

  for (let i = 0; i < len; i++) {
    // 收缩窗口 - 缩 1 格
    if (i !== 0) set.delete(s[i - 1])
    // 扩展窗口 - 尽可能多扩展
    while (end + 1 < len && !set.has(s[end + 1])) {
      set.add(s[end + 1])
      end++
    }
    ans = Math.max(ans, set.size)
  }
  return ans
}

function lengthOfLongestSubstring(s: string): number {
  const len = s.length
  const set = new Set<string>()

  let ans = 0
  let end = -1

  for (let i = 0; i < len; i++) {
    if (i !== 0) set.delete(s[i - 1])
    while (end + 1 < len && !set.has(s[end + 1])) {
      set.add(s[end + 1])
      end++
    }
    ans = Math.max(ans, set.size)
  }

  return ans
}

Details

时间复杂度： $O (n)$
空间复杂度： $O (n)$
原理简述
- 收缩窗口：start 移动，start 扫过的区域，全部都从 set 集合中移除 set.delete(...)。
- 扩展窗口：end 移动，end 扫过的区域，全部都丢到 set 集合中 set.add(...)。
- 和上述“solutions.1 - 暴力解法”非常类似，不同点在于 end 指针的移动不再是从 start 开始，而是基于上一次的位置开始。
end = -1、end 的移动逻辑
- end 移动时，意味着扩展窗口。但是 end 每次移动之前，需要处理的逻辑：
  1. 判断下一个位置是否还有成员，如果没有，则不移动；否则进入下一步。
  2. 判断下一个位置的成员是否已经在哈希表中存在，若存在，则不移动；否则进入下一步。
  3. 将下一个成员加入到哈希表中
  4. 重复以上步骤
- end 开始赋值为 -1，也是为了让代码更优雅，好从字符串下标 0 的位置开始判断。
记录结果的两个时刻：
1. 在每次收缩窗口之前
2. 在遍历完字符串的时候
1.js vs. 2.js
- 两者的原理基本相同
- 1.js 中，外层循环跑一次，窗口的尺寸只可能会变化一格。
- 2.js 中，外层循环跑一次，窗口的尺寸可能会变化多格。

0003. 无重复字符的最长子串【中等】 ​

1. 📝 Description ​

2. 💻 solutions.1 - 暴力解法 ​

3. 💻 solutions.2 - 滑动窗口 ​

🫧 Discussions

0003. 无重复字符的最长子串【中等】

1. 📝 Description

2. 💻 solutions.1 - 暴力解法

3. 💻 solutions.2 - 滑动窗口