0053. 最大子数组和【中等】
1. 📝 Description
leetcode
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
子数组
是数组中的一个连续部分。
示例 1：
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。示例 2：
输入：nums = [1]
输出：1示例 3：
输入：nums = [5,4,-1,7,8]
输出：23提示：
1 <= nums.length <= 10^5-10^4 <= nums[i] <= 10^4
进阶： 如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。
2. 💻 题解.1 - 暴力解法
javascript
var maxSubArray = function(nums) {
const len = nums.length;
if(len === 1) return nums[0];
let ans = Math.min(...nums); // 有可能 nums 都是负数
for (let i = 0; i < len; i++) {
let count = 0;
for (let j = i; j < len; j++) {
count += nums[j];
ans = Math.max(count, ans);
}
}
return ans;
};- 思想很简单，就是两层循环，将所有可能的子数组都判断一遍，取最值。
- 注：回看提交记录时，发现一开始是通过的，但是现在运行提示超时，应该是新增了一些测试用例，对于一些新的测试用例，该暴力解法在执行后被判定为超时。
3. 💻 题解.2 - 动态规划
javascript
var maxSubArray = function(nums) {
let sum = 0, ans = nums[0];
for (let i = 0; i < nums.length; i++) {
sum = Math.max(sum + nums[i], nums[i]);
ans = Math.max(ans, sum);
}
return ans;
};- 动态规划
- 在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线。这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法。
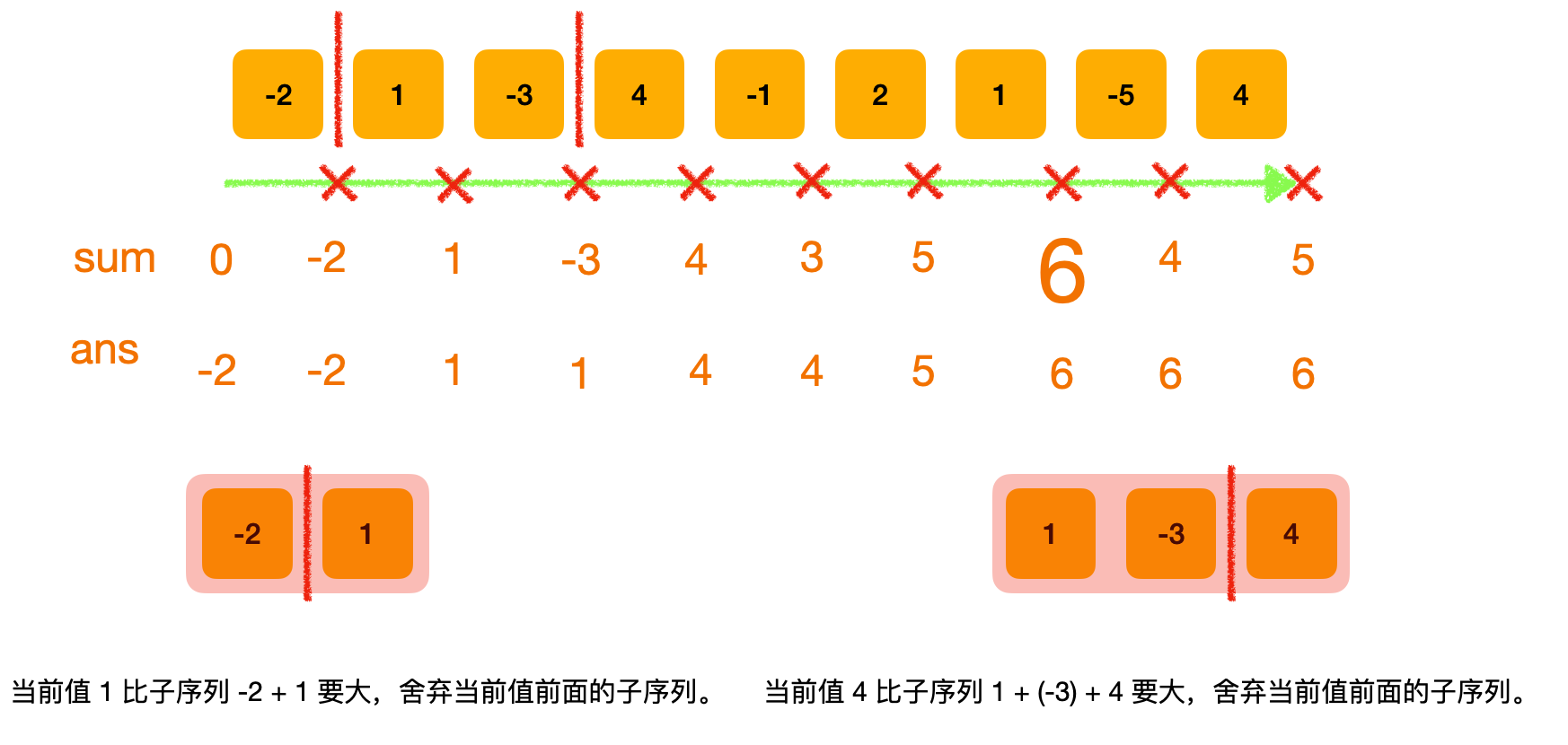
- 若一个连续子序列的最后一个元素，比这个序列的和还要大。这意味着，最大的连续子序列不可能包含前面部分，直接将其舍弃即可。