0007. 整数反转【中等】

• 1. 📝 Description
• 2. 💻 题解.1 - 暴力解法（转为字符串求解）
• 3. 💻 题解.2 - 数学方法
• 4. 📒 Math.trunc 的基本用法
• 5. 🤖 markdown 书写数学公式的语法
  • 5.1. 内联公式
  • 5.2. 独立行公式（块级公式）
  • 5.3. 常见的 LaTeX 数学符号
  • 5.4. 示例
• 6. 🤖 整数位数和它的大小之间对数关系
• 7. 🤖 对比 $O(lo{g}_{10}N)$ 和 $O(logN)$

1. 📝 Description

leetcode

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围  [−2³¹,  2³¹ − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

• 输入：x = 123
• 输出：321

示例 2：

• 输入：x = -123
• 输出：-321

示例 3：

• 输入：x = 120
• 输出：21

示例 4：

• 输入：x = 0
• 输出：0

提示：

• -2<sup>31</sup> <= x <= 2<sup>31</sup> - 1

2. 💻 题解.1 - 暴力解法（转为字符串求解）

var reverse = function (x) {
  let ans
  if (x < 0) {
    // x 为负数
    ans = '-' + x.toString().substring(1).split('').reverse().join('') - 0
  } else {
    // x 为正数
    ans = x.toString().split('').reverse().join('') - 0
  }

  const max = 2 ** 31 - 1
  const min = -(2 ** 31)

  if (ans < min || ans > max) {
    return 0
  } else {
    return ans
  }
}

Details

• 时间复杂度：O(n)
• 空间复杂度：O(n)

其中 n 是整数 x 转换为字符串后的字符数，字符串操作过程中生成了多个长度为 n 的中间结果，时间和空间消耗主要集中在这些字符串操作上。

这种转为字符串的处理方案，优点在于易理解，缺点在于性能不佳。字符串操作相对于纯数学运算会有较高的时间和空间开销，对于大数可能会影响性能。

上述做法还依赖于特定语言的字符串处理能力，不具有普遍性。在某些低级语言或环境中可能不适用，需要手写高级语言预设的 API（比如 toString、substring、split 等）的功能。

注意：

x.toString().split('').reverse().join('') - 0 这种隐式类型转换的写法，在 js 中 OK，但是在 ts 中默认是不被允许的，可以使用显示转换的写法 Number(x.toString().split('').reverse().join(''))

3. 💻 题解.2 - 数学方法

记录： 作图的时候，平板横屏看，感觉图的大小刚好，如果是在手机或者 PC 上预览（限制宽度的话），显然偏小了很多，需要放大来看。接下来作图的时候尽可能不要横向扩展 —— 把宽度弄得太宽，可以纵向扩展 - 让图片长一些，这样预览的效果也许会更好一些。

var reverse = function (x) {
  const min = -Math.pow(2, 31)
  const max = Math.pow(2, 31) - 1
  let ans = 0
  while (x !== 0) {
    ans = ans * 10 + (x % 10)
    x = Math.trunc(x / 10)
  }
  if (ans < min || ans > max) {
    return 0
  } else {
    return ans
  }
}

Details

• 时间复杂度：O(logN)

函数的核心是一个 while 循环，循环的次数由整数 x 的位数决定。假设 x 有 d 位，则循环执行 d 次。因此，时间复杂度为 O(d)。由于一个整数的位数与它的大小是对数关系，若 x 的绝对值为 N，则 d = log10 N，因此时间复杂度可以表示为 O(log10 N)。在大多数分析中，我们用自然对数，所以时间复杂度也可以表示为 O(log N)。

• 空间复杂度：O(1)

没有使用任何额外的数据结构（如数组或对象），所有操作都是就地进行的。因此，空间复杂度为 O(1)。

---

原理简述：

每一次遍历，都将 x 的最低位搬运到 ans 的最高位。

• ans = ans * 10 + x % 10;
• x = Math.trunc(x / 10);

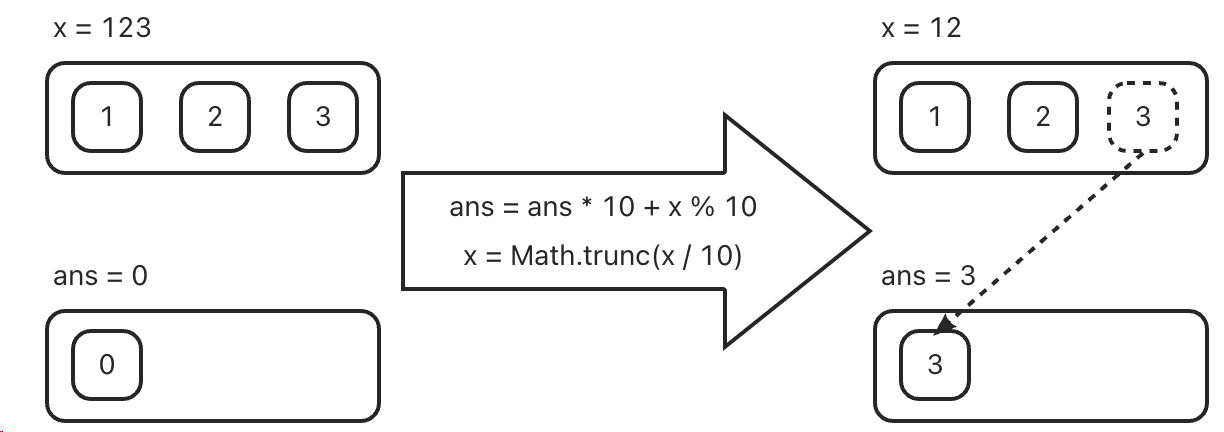
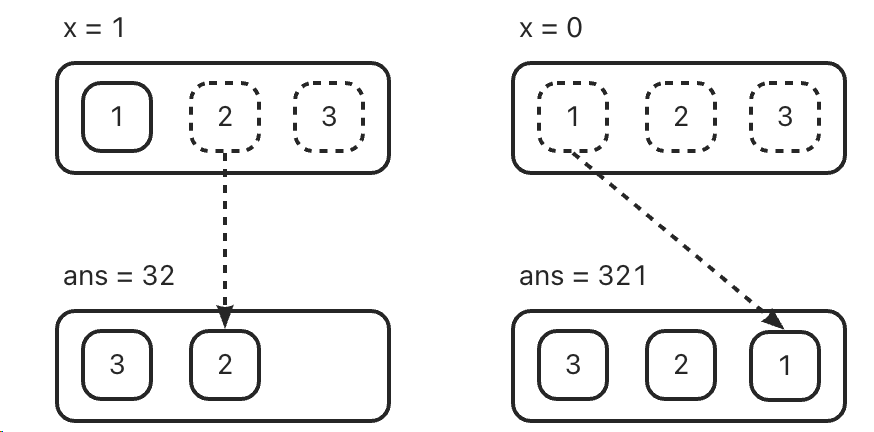
4. 📒 Math.trunc 的基本用法

在 Math.trunc 中，trunc 的全称是 truncate（v. 截短，缩短 英 /'trʌŋkeɪt/ 美 /trʌŋ'ket/）。Math.trunc 方法用于截取数字的小数部分，只保留其整数部分，无论数字是正数还是负数。

console.log(Math.trunc(4.9)) // 输出: 4
console.log(Math.trunc(-4.9)) // 输出: -4
console.log(Math.trunc(4.1)) // 输出: 4
console.log(Math.trunc(-4.1)) // 输出: -4

Math.trunc 会简单地删除小数点后的所有内容，而不会进行舍入操作。这与 Math.floor 和 Math.ceil 的行为不同，Math.floor 总是向下舍入到最接近的整数，Math.ceil 总是向上舍入到最接近的整数。

5. 🤖 markdown 书写数学公式的语法

在 Markdown 中书写数学公式，通常会使用 LaTeX 语法。许多 Markdown 解析器支持通过特定的分隔符来包含 LaTeX 数学表达式。以下是一些常见的方法和示例：

5.1. 内联公式

内联公式是指嵌入到文本中的公式，可以使用单个美元符号 $ 或反引号加 latex 来包裹公式。

• 单个美元符号：这是最常见的方式。

  Euler's identity is $e^{i\pi} + 1 = 0$.

• 反引号加 latex：这种方法在一些 Markdown 编辑器中被支持，例如 GitHub 的 Markdown。

  Euler's identity is `\( e^{i\pi} + 1 = 0 \)`.

5.2. 独立行公式（块级公式）

独立行公式是指单独成行显示的公式，通常使用双美元符号 $$ 或反引号加 latex 来包裹公式。

• 双美元符号：

  $$ E = mc^2 $$

• 反引号加 latex：

  $$
  E = mc^2
  $$

5.3. 常见的 LaTeX 数学符号

• 上标和下标：

  • 上标: x^2
  • 下标: x_2

• 分数：

  • \frac{a}{b}

• 根号：

  • 平方根: \sqrt{x}
  • n 次方根: \sqrt[n]{x}

• 求和符号：

  • \sum_{i=1}^{n} x_i

• 积分符号：

  • \int_{a}^{b} f(x) dx

• 希腊字母：

  • 小写 alpha: \alpha
  • 大写 Alpha: \Alpha
  • 其他希腊字母类似，只需替换相应的字母名。

• 特殊函数：

  • 对数: \log x
  • 自然对数: \ln x
  • 正弦: \sin x
  • 余弦: \cos x
  • 正切: \tan x

• 矩阵：

  \begin{pmatrix}
  a & b \\
  c & d
  \end{pmatrix}

• 多行公式：

  \begin{align*}
  a &= b + c \\
  d &= e + f
  \end{align*}

5.4. 示例

Euler's identity is $e^{i\pi} + 1 = 0$.

The quadratic formula is:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

A matrix:

$$
\begin{pmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{pmatrix}
$$

A system of equations:
\begin{align*}
x + y &= 2 \\
2x - y &= 4
\end{align*}

这些示例应该能够帮助你在 Markdown 中正确地书写数学公式。如果你使用的 Markdown 解析器不直接支持 LaTeX 语法，你可能需要查看该解析器的具体文档，了解它支持的数学公式格式。

6. 🤖 整数位数和它的大小之间对数关系

7. 🤖 对比 $O(lo{g}_{10}N)$ 和 $O(logN)$